Unidad I
Unidad II
Unidad III
es.slideshare.net/willaren/regla-de-la-cadena-y-regla-de-la-potencia
Unidad IV
Unidad V
 la elasticidad,
la elasticidad, 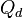 la cantidad demandada y
la cantidad demandada y  el precio:
el precio: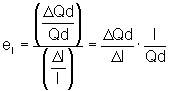
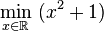
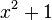 , cuando x se selecciona del conjunto de números reales
, cuando x se selecciona del conjunto de números reales  . El valor mínimo en este caso es
. El valor mínimo en este caso es  y ocurre para
y ocurre para  .
.
| Definición de concavidad | |
| Se dice que la gráfica de una función f es cóncava hacia arriba en un intervalo A, |
 |
 es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
. una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
 , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.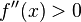 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
. , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada. .
. un punto crítico de una función
un punto crítico de una función  que es continua en
que es continua en que contiene a
que contiene a  . Si
. Si  es derivable en
es derivable en  , entonces
, entonces  puede
puede '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
. '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
. '
' es positiva en ambos lados de
es positiva en ambos lados de  o negativa en ambos lados de c, entonces
o negativa en ambos lados de c, entonces  no es ni un mínimo ni un máximo relativo.
no es ni un mínimo ni un máximo relativo.